Ternary search

Ternary Search is a divide-and-conquer algorithm designed for efficiently finding the position of a target value in a sorted array. It works by separating the array into three parts and recursively narrowing down the search space until the target is found or not.

How it Works:

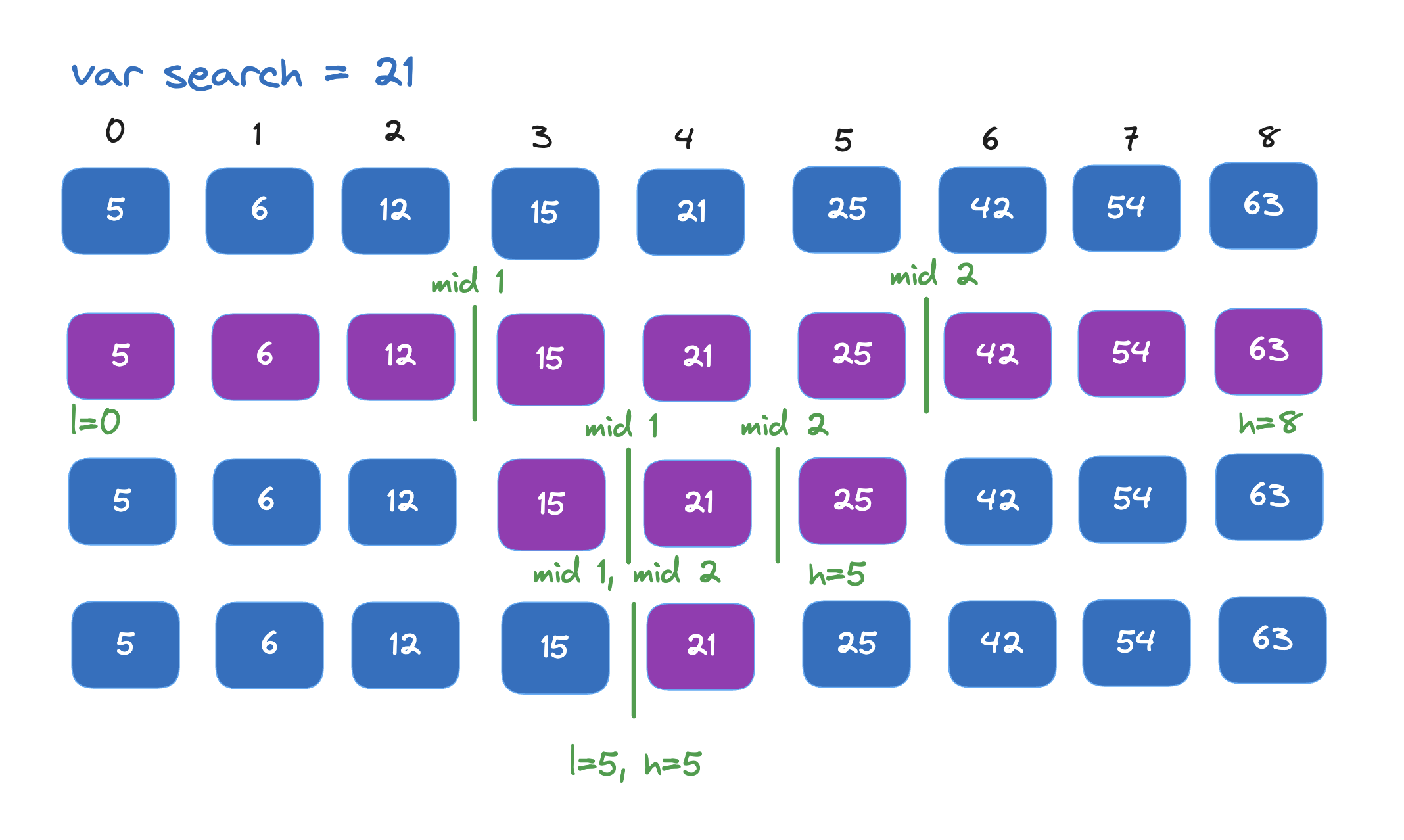
Step 1: Divide the sorted array into three parts.

Step 2: Then compare the target value with the elements at two points within the array, separating it into three segments. If the target is found at one of these points, the search is successful.

Step 3: Based on the comparisons, Ternary Search identifies whether the target lies in the first, second, or third segment of the array.

Step 4: The algorithm then recursively applies the same process to the identified segment. This recursion continues until the target is found or the search space is reduced to an empty array, indicating that the target is not present.

Key Characteristics:

Divide and Conquer Approach: Ternary search follows the “divide and conquer” paradigm. It repeatedly divides the search interval into three parts and narrows down the search space based on the value being searched for.

Applicability: Ternary search is applicable only on sorted arrays or functions that are unimodal (i.e., having a single peak or trough). It’s commonly used to find the maximum or minimum value of a unimodal function.

Comparison Count: Ternary search reduces the size of the search space by one-third in each iteration, which means it usually performs fewer comparisons compared to binary search, especially when the desired element is closer to the ends of the array.

Implementation: Ternary search can be implemented recursively or iteratively. The recursive implementation is straightforward and elegant, but it might suffer from stack overflow for large input sizes. The iterative implementation, on the other hand, is more efficient in terms of space.

Mid-Point Calculation: In each iteration, ternary search calculates two mid-points (m1 and m2) to divide the search space into three equal parts. The value of the mid-points is calculated as follows: $m1 = \text{start} + \frac{\text{end} - \text{start}}{3}$ and $m2 = \text{end} - \frac{\text{end} - \text{start}}{3}$.n.

Space Complexity: Ternary search has a space complexity of $O(1)$ since it does not require any extra space proportional to the input size beyond a few variables used for indices and comparison values.

Applications:

Finding Local Extrema: Ternary search is commonly used to find the maximum or minimum value of a unimodal function over a given interval. This application arises in various fields such as optimization problems, mathematical modeling, and computer graphics.

Finding a Peak in Peak Finding Problem: In a 1D peak finding problem where a peak is defined as an element greater than or equal to its neighbors, ternary search can efficiently locate a peak in $O(\log_3{n})$ time complexity, where $n$ is the size of the array.

Optimizing Functions: Ternary search can be applied in optimization problems where a function needs to be optimized within a certain range. For example, in numerical methods like Newton’s one or gradient descent, the algorithm can help refine the search for the optimal solution.

Searching in Sorted Arrays with Large Number of Comparisons: Ternary search can be advantageous in scenarios where the number of comparisons required for binary one becomes too high due to the nature of the data. The algorithm reduces the number of comparisons needed by approximately one-third in each iteration, potentially leading to faster search times.

Approximate Search: Ternary search can also be adapted for approximate tasks where finding an exact match is not necessary. For example, in databases or search engines, the algorithm can efficiently narrow down the search space for approximate matches, reducing the computational cost.

Finding Roots of Equations: The algorithm can be applied in numerical analysis to find roots of equations within a certain interval. Although methods like Newton’s method are more commonly used for this purpose, ternary search can provide an alternative approach, especially when the function is not differentiable or its derivative is difficult to compute.

Time Complexity:

Ternary Search has a time complexity of O(log3 n), where ‘n’ is the size of the array. This is an improvement over binary search when the search space can be significantly reduced at each step. However, it’s worth noting that constant factors play a role, and in practice, binary search might be faster for smaller datasets due to simpler arithmetic operations. Ternary Search is particularly beneficial when the dataset is large and the space can be significantly reduced with each iteration.

Example

function ternarySearch(
  func: (x: number) => number,
  left: number,
  right: number,
  epsilon: number
): number {
  while (right - left > epsilon) {
    const mid1 = left + (right - left) / 3;
    const mid2 = right - (right - left) / 3;

    const value1 = func(mid1);
    const value2 = func(mid2);

    if (value1 < value2) {
      left = mid1;
    } else {
      right = mid2;
    }
  }

  return (left + right) / 2;
}