Selection sort

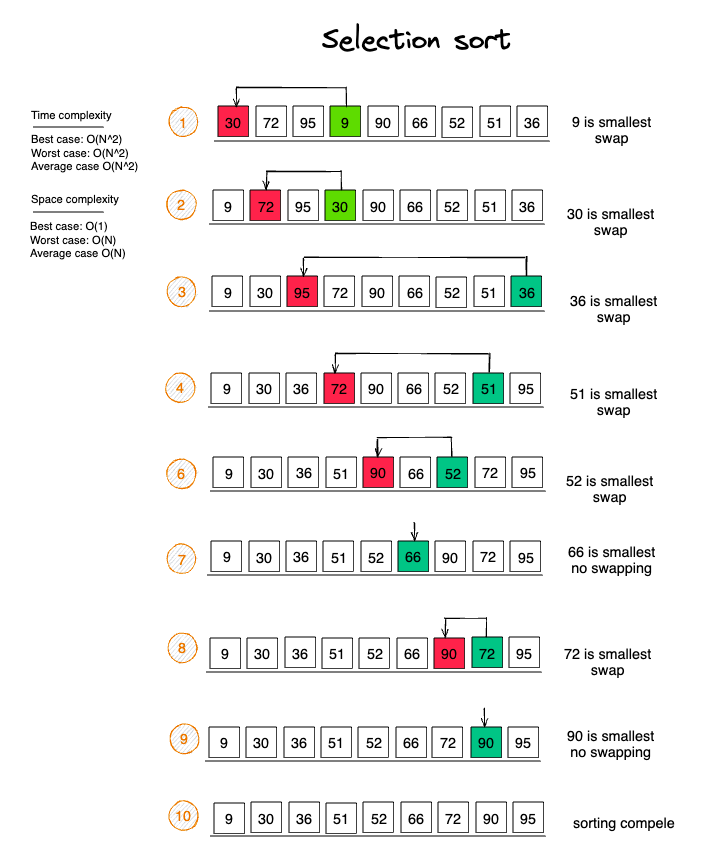
Selection sort is a simple and efficient sorting algorithm that works by repeatedly selecting the smallest (or largest) element from the unsorted portion of the list and moving it to the sorted portion of the list.

How it works:

Step 1: Start with an unsorted list/array of elements.

Step 2: Repeat until the entire list is sorted: Find the minimum element in the unsorted portion and swap the minimum element with the leftmost element.

Step 3: Move the boundary between the portions one position to the right.

Step 4: Continue this process until the entire list is sorted.

Step 5: Once all elements are sorted, the process ends, and you have a fully ready list.

Key Characteristics:

Basic Algorithm: Selection sort divides the input list into a sorted and an unsorted region, repeatedly selects the smallest (or largest) element from the unsorted region and swaps it with the leftmost unsorted element.

In-place Sorting: Sorts elements by swapping them in place within the array or list.

Not Adaptive: Selection sort’s performance doesn’t improve even if the input is partially sorted.

Not Stable: May change the relative order of equal elements.

Simple Implementation: Easy to understand and implement.

Inefficient for Large Datasets: Due to its quadratic time complexity, it’s inefficient for large datasets compared to more efficient algorithms like quicksort or mergesort.

Applications:

Educational Purposes: Selection sort is commonly used in educational settings to teach sorting algorithms due to its simplicity.

Small Datasets: Suitable for sorting small datasets where simplicity is prioritized over efficiency.

Embedded Systems: Can be used in environments with limited resources for sorting small arrays due to its simplicity and minimal memory requirements.

Testing and Debugging: Useful for quick implementation and verification of sorting functionality in software development.

Ad Hoc Sorting: Provides a simple and quick solution for one-time or temporary sorting needs in situations where efficiency is not critical.

Time complexity:

The time complexity of selection sort is O(n^2), where n is the number of elements in the array, due to its nested loops. The outer loop iterates through each element, and the inner loop searches for the minimum element in the unsorted portion, both running n times. This results in a quadratic time complexity of O(n^2), making selection sort less efficient for large datasets compared to other sorting algorithms.

Example:

function selectionSort(array: any[]) {
  for (let i = 0; i < array.length - 1; i++) {
    let min = i;
    for (let j = i + 1; j < array.length; j++) {
      if (array[min] > array[j]) min = j;
    }
    [array[i], array[min]] = [array[min], array[i]];
  }
  return array;
}

	public static void selectionSort(int[] array) {
		for(int i = 0; i < array.length - 1; i++) {
			int min = i;
			for(int j = i + 1; j < array.length; j++) {
				if(array[min] > array[j]) {
					min = j;
				}
			}
			int temp = array[i];
			array[i] = array[min];
			array[min] = temp;
		}
	}

print('This is selection sort')

def find_smallest(arr):
    smallest = arr[0]
    smallest_index = 0
    for i in range(1, len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest_index

def selection_sort(arr):
    newArr = []
    for i in range(len(arr)):
        smallest = find_smallest(arr)
        newArr.append(arr.pop(smallest))
    return newArr