Quicksort
Quick Sort is an efficient, comparison-based sorting algorithm that follows the divide-and-conquer paradigm. It works by selecting a “pivot” element from the array and partitioning the other elements into two sub-arrays according to whether they are less than or greater than the pivot. The sub-arrays are then recursively sorted.
How it works:
Step 1: Select a pivot. It might be any element at random, the first or last element, middle one.
Step 2: Partition the array around the pivot element. Move all the elements that less than pivot to the left of the it and move all elements that more or equal to the right side.
Step 3: After Step 2, the pivot element is in its correct position
Step 4: Apply the quicksort recursively on the left partition and then on the right partition
Step 5: Stop recursion when array is sorted when reach out the base case. It’s an array of zero or one element.
Key Characteristics:
Divide and Conquer: it is a divide-and-conquer algorithm that partitions the array into smaller sub-arrays, sorts each of them recursively, and then combines them to obtain a sorted array.
In-place Sorting: Quick Sort often sorts elements in place within the array, which means it does not require additional memory beyond a few stack frames for recursion.
Unstable: The algorithm is generally an unstable, meaning that it may change the relative order of equal elements.
Efficiency: Quick Sort is highly efficient for large datasets due to its average-case time complexity of O(n log n). It outperforms many other sorting algorithms like Bubble Sort, Insertion Sort, and Selection Sort for larger datasets.
Pivot Selection: It’s efficiency heavily relies on the selection of a good pivot element, which partitions the array into smaller sub-arrays. Common strategies for pivot selection include choosing the first, last, or middle element of the array, or using techniques like median-of-three.
Adaptive: The algorithm is adaptive, meaning that it performs better when the input data is partially sorted. This adaptability can lead to improved performance in many real-world scenarios.
Parallelizability: Quick Sort is easily parallelizable, which means it can take advantage of multiple processors or threads to sort data more quickly.
Applications:
General Sorting: Quick Sort is widely used for sorting large datasets efficiently in various software applications, including databases, operating systems, and programming languages.
Programming Competitions: It is a popular choice for sorting algorithms in programming competitions due to its efficiency and ease of implementation.
Libraries and Frameworks: The algorithm is often implemented in standard libraries and frameworks for sorting data structures like arrays, lists, and trees.
Online Sorting: Quick Sort’s efficiency makes it suitable for online sorting scenarios where new data is continuously arriving and needs to be sorted quickly.
Data Analysis: It is utilized in data analysis tasks where sorting large datasets is a common requirement, such as in data mining, machine learning, and statistical analysis.
Operating Systems: It is used in various components of operating systems for tasks like file system management and memory allocation.
Numerical Methods: The algorithm can be applied in numerical methods and scientific computing for sorting arrays of numerical data efficiently.
Network Routing: Quick Sort is used in network routing algorithms for organizing and sorting routing tables efficiently.
Time Complexity:
Quick Sort has an average and best-case time complexity of O(n log n), where ‘n’ is the number of elements in the array. In the worst case, it is O(n^2), but this is rare when a good pivot selection strategy is used. This algorithm is often faster in practice than other O(n log n) ones, and it is widely used in various applications due to its efficiency.
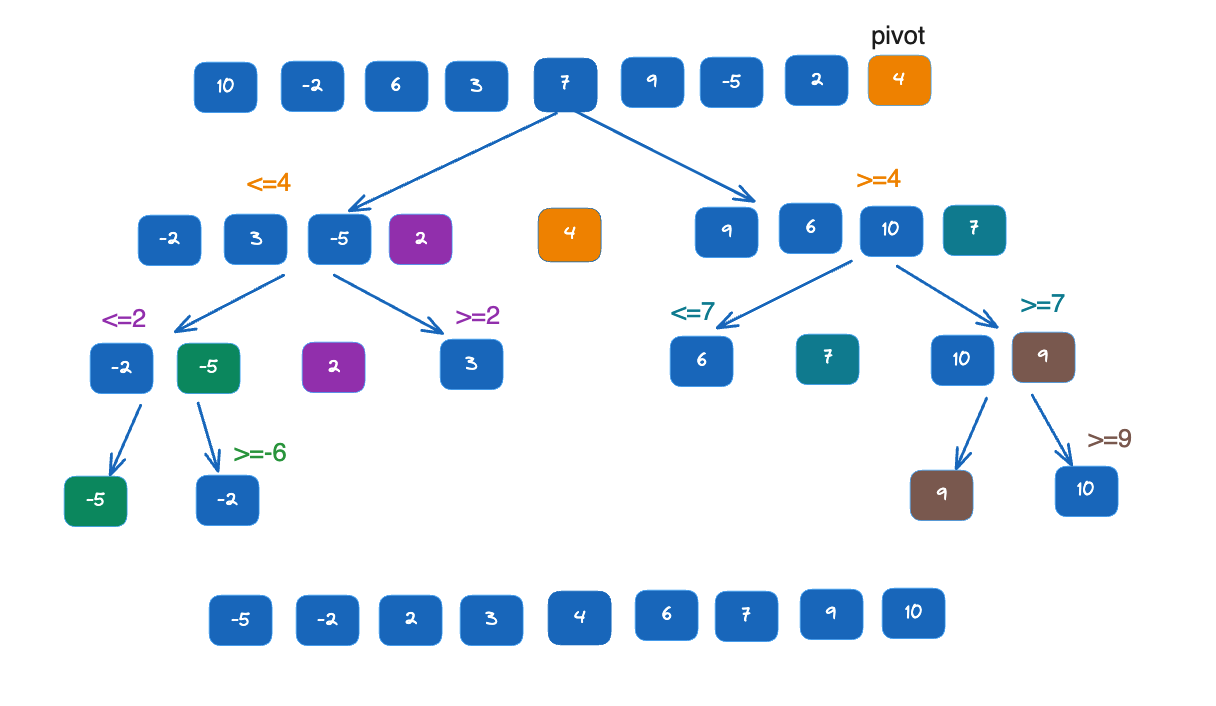
Example:
class Solution {
int makePartition(int [] arr, int low, int high) {
int pivot = arr[high];
int currentIndex = low - 1;
for(int i = low; i < high; i++) {
if(arr[i] < pivot) {
currentIndex++;
int temp = arr[i];
arr[i] = arr[currentIndex];
arr[currentIndex] = temp;
}
}
int temp = arr[high];
arr[high] = arr[currentIndex + 1];
arr[currentIndex + 1] = temp;
return currentIndex + 1;
}
void quicksort(int[] arr, int low, int high) {
if(low < high) {
int pivot = makePartition(arr, low, high);
quicksort(arr, low, pivot - 1);
quicksort(arr, pivot + 1, high);
}
}
void quickSort (int[] arr) {
int n = arr.length;
quicksort(arr, 0, n - 1);
}
}
def quicksort(arr):
if len(arr) < 2:
return arr
else:
pivot = arr[len(arr)/2]
less = [i for i in arr[1:] if i <= pivot]
greater = [i for i in arr[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)
print(quicksort([10,2,3,1,5,4]))
class Solution {
static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
private static void quickSort(int[] array, int start, int end) {
if(end <= start) return; // base case
int pivot = partition(array, start, end);
quickSort(array, start, pivot -1);
quickSort(array, pivot + 1, end);
}
private static int partition(int[] array, int start, int end) {
int pivot = array[end];
int i = start - 1;
for(int j = start; j <= end -1; j++) {
if(array[j] < pivot) {
i++;
swap(array, i, j);
}
}
i++;
swap(array, i, end);
return i;
}
}
function quicksort(arr: number[]): number[] {
if (arr.length < 2) {
return arr;
} else {
const pivot = arr[Math.floor(arr.length / 2)];
const less = arr.slice(1).filter((i) => i <= pivot);
const greater = arr.slice(1).filter((i) => i > pivot);
return [...quicksort(less), pivot, ...quicksort(greater)];
}
}
function quicksort(arr: number[]): number[] {
if (arr.length < 2) {
return arr;
} else {
const pivot = arr[Math.floor(arr.length / 2)];
const less: number[] = [];
const equal: number[] = [];
const greater: number[] = [];
for (let i = 0; i < arr.length; i++) {
if (arr[i] < pivot) {
less.push(arr[i]);
} else if (arr[i] === pivot) {
equal.push(arr[i]);
} else {
greater.push(arr[i]);
}
}
return [...quicksort(less), ...equal, ...quicksort(greater)];
}
}