Merge sort

Merge Sort is a comparison-based sorting algorithm that follows the divide-and-conquer paradigm. It works by dividing the unsorted array into ‘n’ sub-arrays, each containing one element. It then repeatedly merges these sub-arrays to produce new sorted ones until there is only one sub-array remaining - the fully sorted array.

How it works:

Step 1: The unsorted array is recursively divided into two halves until each sub-array contains only one element. This is the base case of the recursion.

Step 2: The adjacent sub-arrays are then recursively merged to produce new sorted ones. This process continues until there is only one sub-array remaining the fully sorted array.

Step 3: The key operation in Merge Sort is the merging of two sorted sub-arrays to produce a single, sorted one. This involves comparing elements from the two sub-arrays and placing them in the correct order.

Key Characteristics:

Divide and Conquer: Merge Sort is a divide-and-conquer algorithm that breaks down the array into smaller sub-arrays, sorts each of them recursively, and then merges the result to final sorted array.

Stable Sorting: It is a stable sorting algorithm, meaning that it preserves the relative order of equal elements during sorting.

Efficient for Large Datasets: This efficient time complexity makes it well-suited for sorting large datasets, outperforming many other sorting algorithms for such scenarios.

In-place vs. Out-of-place: While Merge Sort can be implemented both in-place (where it sorts the array within its original memory space) and out-of-place (where it requires additional memory space), the out-of-place implementation is more common due to its simplicity and efficiency.

Parallelizability: The algorithm can be parallelized easily, allowing it to take advantage of multiple processors or threads for faster sorting of data.

Space Complexity: Merge Sort typically has a space complexity of O(n), as it requires additional memory space for the temporary arrays used during the merging process.

Reliable Performance: Merge Sort’s consistent time complexity and stable sorting make it a reliable choice for applications where predictable performance and stability are essential.

Applications:

Sorting Large Datasets: Merge Sort is highly efficient for sorting large datasets, making it suitable for various applications where sorting a significant amount of data is required. This includes tasks like sorting database records, organizing files on disk, or processing large sets of data in scientific research.

External Sorting: It is commonly used in external sorting algorithms where data is too large to fit into memory entirely. It efficiently sorts data stored on external storage devices like hard drives by dividing it into manageable chunks, sorting them in memory, and then merging them back together.

Network Routing: Merge sort is utilized in network routing algorithms for organizing and sorting routing tables efficiently. In networking applications, sorting large sets of routing information is crucial for optimizing data transmission and network performance.

Parallel Processing: Its divide-and-conquer approach lends itself well to parallel processing. It can be parallelized across multiple processors or threads, allowing for faster sorting of data in parallel computing environments.

Optimizing Data Processing Pipelines: Merge Sort can be used in data processing pipelines to efficiently sort and merge streams of data from different sources. This is common in real-time data analytics, where sorted data is essential for performing efficient queries and analyses.

Operating Systems: It is employed in various components of operating systems for tasks like sorting file directories, managing memory allocation, and organizing system resources efficiently.

Time Complexity:

Merge Sort has a consistent time complexity of O(n log n) in all cases, where ‘n’ is the number of elements in the array. It is a stable sorting algorithm, meaning that equal elements maintain their relative order in the sorted output. While Merge Sort has a slightly higher space complexity due to the need for additional memory, its stability and predictable performance make it a widely used and reliable sorting algorithm.

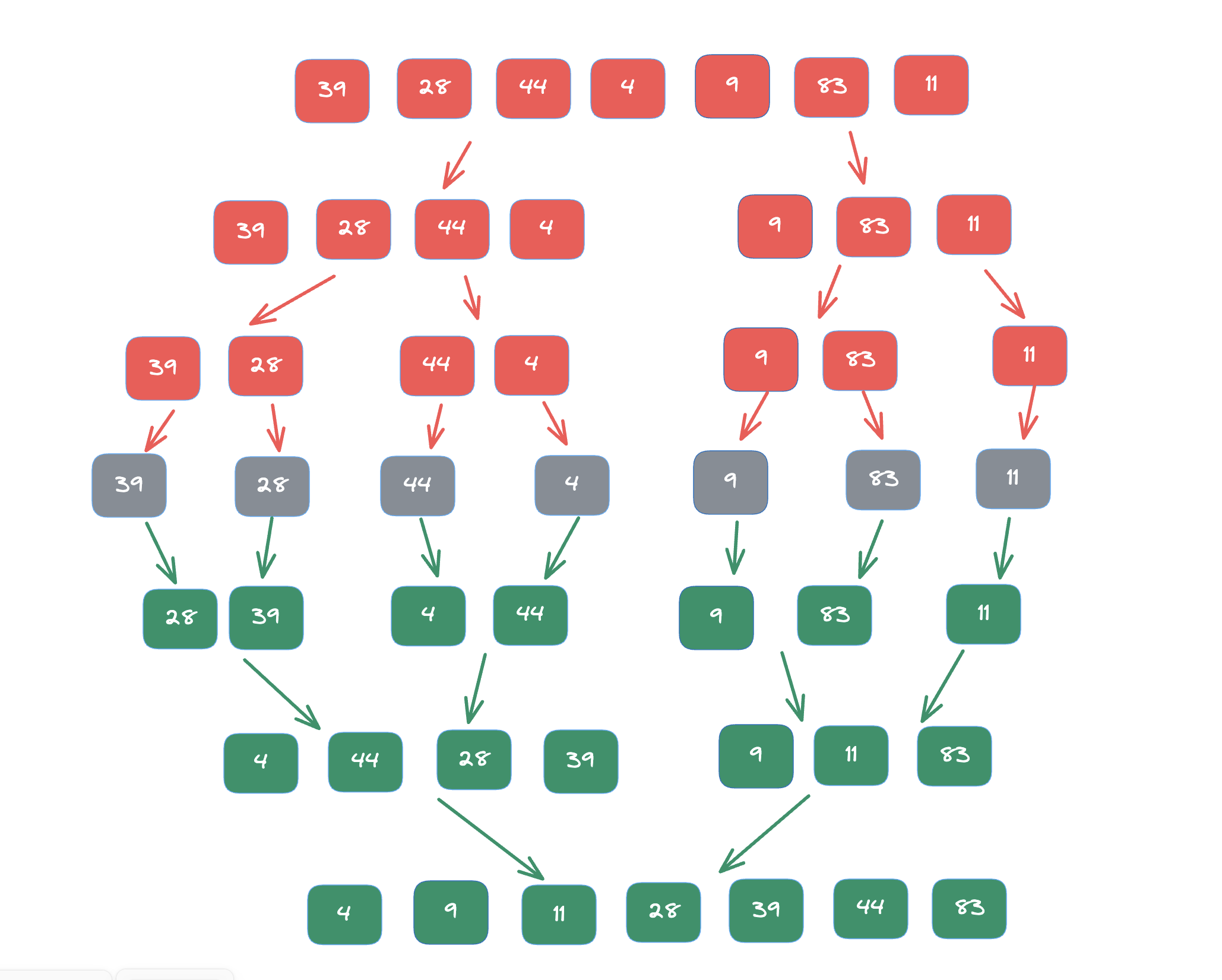
Example:

class Solution {

	void merge(int[] arr, int low, int mid, int high) {
		int subArr1Size = mid - low + 1;
		int subArr2Size = high - mid;

		int [] subArr1 = new int[subArr1Size];
		int [] subArr2 = new int[subArr2Size];

		for (int i = 0; i < subArr1Size; i++) {
           subArr1[i] = arr[low + i];
      	 }
      	 for (int i = 0; i < subArr2Size; i++) {
           subArr2[i] = arr[mid + 1 + i];
		}
		int i = 0, j = 0, k = low;

		while(i < subArr1Size && j < subArr2Size) {
			if(subArr1[i] <= subArr2[j]) {
				arr[k] = subArr1[i];
				i++;
			} else {
				arr[k] = subArr2[j];
				j++;
			}
			k++;
		}
		while(i < subArr1Size) {
			arr[k++] = subArr1[i++];
		}
		while (j < subArr2Size) {
           arr[k++] = subArr2[j++];
       }
	}

	void mergesort(int[] arr, int low, int high){
		if(high > low) {
			int mid = (high + low) / 2;
			mergesort(arr, low, mid);
			mergesort(arr, mid + 1, high);
			merge(arr, low, mid, high);
		}
	}

	void mergeSort (int[] arr) {
		int n = arr.length;
		mergesort(arr, 0, n - 1);
	}
}

function mergeSort(arr: number[]): number[] {
  if (arr.length <= 1) {
    return arr;
  }

  const middle = Math.floor(arr.length / 2);
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);

  return merge(mergeSort(left), mergeSort(right));
}

function merge(left: number[], right: number[]): number[] {
  let result: number[] = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] < right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex));
}