Interpolation search

Interpolation Search is a an algorithm designed for finding a specific target value in a sorted array. Unlike linear or binary search, this algorithm utilizes the characteristics of the data distribution to make more informed decisions about where to look for the target. It is particularly effective when the data has a uniform distribution.

How it works:

Step 1: It utilizes linear interpolation to estimate the likely position of the target value in the array.

Step 2: Instead of evenly dividing the search space, as in binary search, the algorithm estimates the probable position of the target based on its value relative to the minimum and maximum values in the array.

Step 3: It calculates an estimate of the target’s position by considering the relative location of the target with respect to the minimum and maximum values in the current search space.

Step 4: Based on the calculated estimate, the algorithm narrows down the search space and repeats the process until the target is found or the search space is exhausted.

Key Characteristics:

Estimation of Position: Interpolation search estimates the probable position of the target value within the array based on the values at the ends of the array. Unlike binary search, which always divides the search space in half, interpolation search calculates a position closer to the target based on the distribution of values in the array.

Requirement of Sorted Array: Similar to binary search, interpolation search requires the input array to be sorted in ascending order. This is necessary to make assumptions about the distribution of values within the array and to perform efficient searches.

Variable Step Size: In interpolation search, the step size for narrowing down the search interval varies depending on the estimated position of the target value. This variable step size allows for more efficient convergence towards the target value compared to fixed step sizes used in binary search.

Calculation of Position: The estimated position of the target value is calculated using interpolation formula, which typically involves linear interpolation. However, other interpolation techniques such as quadratic or exponential interpolation can also be used depending on the nature of the data.

Complexity: The time complexity of interpolation search is $O(\log \log n)$ on average, where $n$ is the number of elements in the array. This complexity is better than binary search in certain scenarios, especially when the elements are uniformly distributed.

Worst-case Scenario: While interpolation search generally performs well, it can degrade to $O(n)$ time complexity in the worst-case scenario, particularly when the distribution of values in the array is highly skewed or uneven.

Handling Non-uniform Distributions: Interpolation search is particularly effective when the values in the array are uniformly distributed. However, in cases where the distribution is non-uniform, interpolation search may not provide significant advantages over other search algorithms like binary search.

Implementation: Interpolation search can be implemented recursively or iteratively. Iterative implementation is often preferred due to its simplicity and efficiency. However, recursive implementation may be more intuitive for some programmers.

Applications:

Numerical Data Retrieval: Interpolation search is commonly used in databases and data retrieval systems where data is stored in sorted arrays. It allows for fast retrieval of numerical data, especially when the values are uniformly distributed.

Scientific Computing: In scientific computing, the algorithm can be applied in scenarios such as searching for specific data points within large datasets or performing numerical simulations where fast access to data is crucial.

Symbol Tables: Interpolation search can be used in symbol tables and compilers for quick retrieval of symbols or identifiers. This is particularly useful in programming languages or applications that deal with large symbol tables.

Searching in Large Datasets: The algorithm can efficiently handle large datasets where binary search may become less efficient due to the fixed step size. It’s used in applications dealing with large volumes of data such as search engines, databases, and data analytics platforms.

Approximate Search: Interpolation search can be adapted for approximate search tasks where finding an exact match is not necessary. For example, in spell checkers or auto-complete features in text editors, interpolation search can quickly narrow down the search space for approximate matches.

Time-Critical Systems: In real-time systems where response time is critical, interpolation search can be beneficial due to its average-case time complexity of $O(\log \log n)$. This makes it suitable for applications requiring fast search operations, such as in financial trading systems or telecommunications networks.

Finding Closest Values: This algorithm can be used to find the closest value to a given target value within a sorted array. This application is useful in scenarios such as image processing, signal processing, and sensor data analysis.

Data Compression and Encoding: Interpolation search algorithms can be used in compression and encoding techniques to efficiently search for patterns or symbols within compressed data streams. This is common in multimedia compression algorithms like JPEG and MPEG.

Geospatial Data Processing: In geographic information systems (GIS) and mapping applications, interpolation search can be used to quickly retrieve spatial data points or locations based on their coordinates, enabling efficient spatial analysis and visualization.

Machine Learning and Data Mining: Interpolation search can be applied in machine learning algorithms and data mining tasks for efficient searching and retrieval of data points during training or querying processes, especially in high-dimensional spaces.

Time Complexity:

The time complexity of Interpolation Search is O(log log n) on average, where “n” is the number of elements in the array. In the best case, it can be O(1), and in the worst case, it can be O(n). However, the average case is often more relevant, and it is O(log log n) under certain assumptions about the distribution of the data.

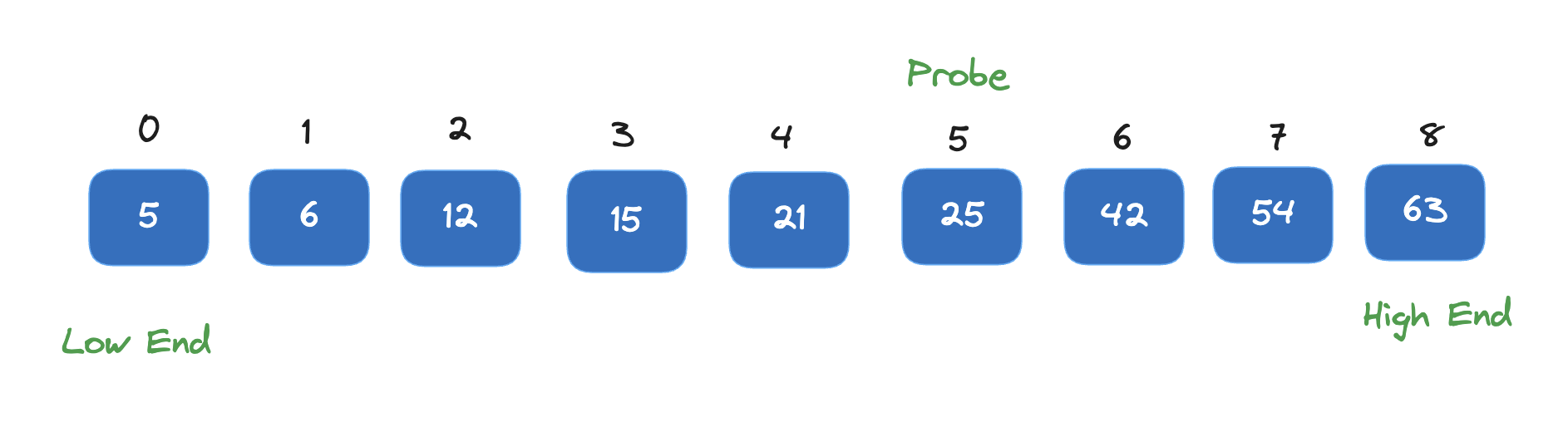
Example

class Solution {

	private static int interpolationSearch(int[] array, int value) {
		int low = 0;
		int high = array.length - 1;

		while(value >=array[low] && value <= array[high] && low <= high) {
			int probe = low + (high - low) * (value - array[low]) / (array[high] - array[low]);
			if(array[probe] == value) {
				return probe;
			} else if(array[probe] > value) {
				low = probe + 1;
			} else {
				high = probe -1;
			}

		}

		return -1;
	}

}

function interpolationSearch(array: number[], value: number): number {
  let low = 0;
  let high = array.length - 1;

  while (value >= array[low] && value <= array[high] && low <= high) {
    const probe =
      low + ((high - low) * (value - array[low])) / (array[high] - array[low]);
    const roundedProbe = Math.floor(probe);

    if (array[roundedProbe] === value) {
      return roundedProbe;
    } else if (array[roundedProbe] < value) {
      low = roundedProbe + 1;
    } else {
      high = roundedProbe - 1;
    }
  }

  return -1;
}