Ford Fulkerson algorithm

The Ford-Fulkerson Algorithm is an iterative method to compute the maximum flow in a flow network. It was initially designed to solve the max-flow min-cut problem, where the objective is to find the maximum amount of flow that can be sent from a designated source to a designated sink in a directed graph. The algorithm iteratively augments paths from the source to the sink, increasing the flow until it reaches its maximum value.

How is works:

Step 1: Begin with an initial flow of zero. Determine the residual graph, which represents the remaining capacity for each edge.

Step 2: Find an augmenting path from the source to the sink in the residual graph. “An augmenting path” is a path with available capacity on all its edges.

Step 3: Determine the maximum flow that can be added along the augmenting path. This is the minimum capacity value of the edges on this.

Step 4: Update the residual graph by subtracting the flow added along the augmenting path and adding the reverse flow.

Step 5: Repeat steps 2-4 until there are no more augmenting paths.

Step 6: The final flow is the maximum flow in the network.

Key Characteristics:

Maximum flow: The Ford-Fulkerson algorithm finds the maximum flow that can be sent from a source node to a sink node in a flow network. This is useful in various applications such as transportation networks, network flow optimization, and resource allocation.

Augmenting paths: The algorithm relies on the concept of augmenting paths, which are paths from the source to the sink that have available capacity for additional flow. It repeatedly finds augmenting paths and increases the flow along those paths until no more augmenting ones can be found.

Residual graph: To efficiently find augmenting paths, the algorithm maintains a residual graph, which represents the remaining capacity on each edge after the current flow has been sent. This allows the method to explore different paths and incrementally increase the flow.

Capacity constraints: The Ford-Fulkerson algorithm respects capacity constraints on edges, ensuring that the flow along each edge does not exceed its maximum capacity. It increases the flow along augmenting paths without violating these constraints.

Termination condition: The algorithm terminates when no more augmenting paths can be found in the residual graph. At this point, the flow obtained is the maximum flow possible in the network.

Applications:

Network flow optimization: The primary application of the Ford-Fulkerson algorithm is in network flow optimization. It is used in various scenarios such as transportation networks, communication networks, and supply chain management to maximize the flow of goods, data, or resources from a source to a destination while respecting capacity constraints.

Maximum flow problems: The algorithm is specifically designed to solve maximum flow problems, where the goal is to determine the maximum amount of flow that can be sent through a network from a source to a sink. This has applications in tasks such as traffic management, fluid dynamics, and resource allocation.

Minimum cut problems: The Ford-Fulkerson algorithm can also be used to solve minimum cut problems, where the objective is to find the smallest set of edges whose removal disconnects the source from the sink in a flow network. Minimum cut problems have applications in network reliability analysis, image segmentation, and clustering algorithms.

Bipartite matching: The algorithm can be applied to solve bipartite matching problems, where the goal is to find the maximum matching between elements of two disjoint sets. This has applications in job assignment, resource allocation, and stable marriage problems.

Telecommunications: Telecommunication networks utilize the Ford-Fulkerson algorithm for optimizing data transmission rates, routing calls through phone networks, and allocating bandwidth efficiently. It ensures that communication networks operate at maximum capacity while maintaining quality of service.

Hydraulic engineering: In hydraulic engineering, the Ford-Fulkerson algorithm can be used to model fluid flow in pipes, channels, and rivers. It helps in designing efficient water distribution systems, flood control measures, and irrigation networks.

Supply chain management: The Ford-Fulkerson algorithm has applications in supply chain management for optimizing inventory management, production scheduling, and distribution networks. It helps in minimizing transportation costs and maximizing throughput in supply chain operations.

Time Complexity:

The time complexity of the Ford-Fulkerson Algorithm is not strictly defined, as it depends on the choice of augmenting paths. In the worst case, the algorithm may not terminate if the paths are not chosen carefully. When implemented with the Edmonds-Karp variant, where the shortest augmenting paths are chosen using Breadth-First Search, the time complexity is (O(VE^2)), where (V) is the number of vertices and (E) is the number of edges.

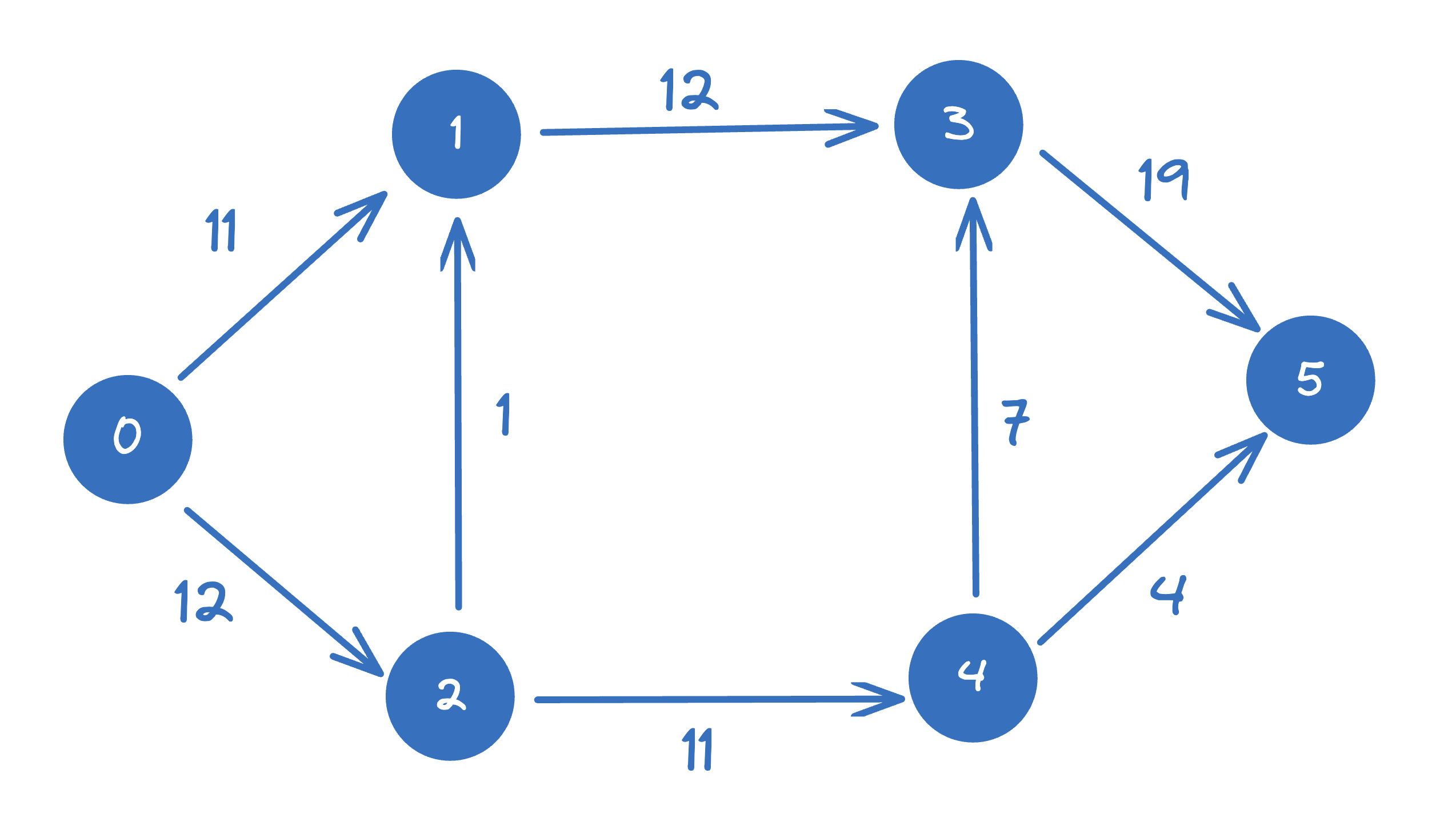
Example:

class FordFulkerson {
  private graph: number[][];
  private numVertices: number;

  constructor(graph: number[][]) {
    this.graph = graph;
    this.numVertices = graph.length;
  }

  fordFulkerson(source: number, sink: number): number {
    let maxFlow = 0;

    // Create a residual graph and initialize it with the original capacities.
    const residualGraph = this.graph.map((row) => [...row]);

    while (true) {
      const path = this.bfs(source, sink, residualGraph);
      if (!path) {
        break; // No augmenting path found, terminate the algorithm
      }

      // Find the minimum capacity along the augmenting path
      let minCapacity = Number.POSITIVE_INFINITY;
      for (let i = 0; i < path.length - 1; i++) {
        const u = path[i];
        const v = path[i + 1];
        minCapacity = Math.min(minCapacity, residualGraph[u][v]);
      }

      // Update residual capacities and reverse edges along the path
      for (let i = 0; i < path.length - 1; i++) {
        const u = path[i];
        const v = path[i + 1];
        residualGraph[u][v] -= minCapacity;
        residualGraph[v][u] += minCapacity;
      }

      // Add the flow of the augmenting path to the total flow
      maxFlow += minCapacity;
    }

    return maxFlow;
  }

  bfs(source: number, sink: number, graph: number[][]): number[] | null {
    const visited: boolean[] = new Array(this.numVertices).fill(false);
    const queue: number[] = [source];
    const parent: number[] = new Array(this.numVertices).fill(-1);

    while (queue.length > 0) {
      const u = queue.shift()!;

      for (let v = 0; v < this.numVertices; v++) {
        if (!visited[v] && graph[u][v] > 0) {
          queue.push(v);
          parent[v] = u;
          visited[v] = true;
        }
      }
    }

    if (!visited[sink]) {
      return null; // No augmenting path found
    }

    const path: number[] = [];
    for (let v = sink; v !== source; v = parent[v]) {
      path.unshift(v);
    }
    path.unshift(source);

    return path;
  }
}

// Example usage:
const graph = [
  [0, 16, 13, 0, 0, 0],
  [0, 0, 10, 12, 0, 0],
  [0, 4, 0, 0, 14, 0],
  [0, 0, 9, 0, 0, 20],
  [0, 0, 0, 7, 0, 4],
  [0, 0, 0, 0, 0, 0],
];

const fordFulkerson = new FordFulkerson(graph);
const maxFlow = fordFulkerson.fordFulkerson(0, 5);
console.log("Maximum Flow:", maxFlow);