Dijkstra’s algorithm

Dijkstra’s algorithm is a graph traversal one used to find the shortest path from a source node to all other ones in a weighted graph. It maintains a set of tentative distances for each node, gradually updating them as it explores the graph. At each step, it selects the node with the smallest tentative distance, visits its neighbors, and updates their tentative distances if a shorter path is found. The algorithm continues until all nodes have been visited or the destination one is reached. Dijkstra’s algorithm is widely used in network routing protocols and pathfinding applications in computer science.

How it works:

Step 1: Set the initial distance to the starting vertex as 0 and all other onces to infinity. Create a priority queue or a min-heap to store vertices based on their current tentative distances.

Step 2: While there are vertices in the priority queue, select the vertex with the smallest tentative distance. Explore its neighbors and update their tentative distances if a shorter path is found.

Step 3: For each neighbor, calculate the sum of the tentative distance to the current vertex and the weight of the edge between them. If this sum is smaller than the current tentative distance to the neighbor, update the tentative distance.

Step 4: Mark the current vertex as visited to avoid redundant calculations.

Step 5: Repeat steps 2-4 until all vertices are visited or the destination vertex is reached.

Step 6: The final result is an array of shortest distances from the starting vertex to all other vertices.

Key Characteristics:

Single-Source Shortest Path: Dijkstra’s algorithm finds the shortest paths from a single source node to all other nodes in a graph with non-negative edge weights.

Greedy Algorithm: The algorithm is a greedy algorithm as it selects the next node to visit based on the shortest known distance from the source node. It iteratively expands the frontier of explored nodes by selecting the node with the smallest tentative distance.

Initialization: Dijkstra’s algorithm initializes the distances from the source node to all other nodes as infinity, except it itself, which is assigned a distance of zero. It also maintains a priority queue (often implemented using a min-heap) to keep track of nodes with the smallest tentative distances.

Relaxation: The algorithm performs relaxation of edges during each iteration. For each node in the priority queue, it considers all its outgoing edges and updates the tentative distance to its neighboring nodes if a shorter path is found through the current node.

Termination: Dijkstra’s algorithm terminates when all nodes have been visited or when the priority queue becomes empty. At termination, the shortest path distances from the source node to all other nodes have been calculated.

Non-Negative Edge Weights: The algorithm requires non-negative edge weights. If negative edge weights are present, the algorithm may not produce correct results.

Space Complexity: The space complexity of Dijkstra’s algorithm is (O(V)) for storing the distances and priority queue, where (V) is the number of vertices in the graph.

Applications:

Routing in Networks: Dijkstra’s algorithm is commonly used in network routing protocols, such as Open Shortest Path First (OSPF) and Intermediate System to Intermediate System (IS-IS). It helps in finding the shortest paths for data packets to traverse through computer networks efficiently. It’s also applicable to Telecommunications Networks

Navigation Systems: The algorithm is used in GPS navigation systems to calculate the shortest routes between locations. It helps in providing users with optimal directions for reaching their destinations while considering factors like traffic congestion and road conditions.

Transportation Networks: Dijkstra’s algorithm is applied in transportation planning and management systems to optimize routes for vehicles, such as buses, taxis, and delivery trucks. It helps in minimizing travel time and fuel consumption while maximizing efficiency.

Airline Route Planning: The algorithm is used in airline route planning systems to determine the shortest paths between airports. It helps airlines in optimizing flight schedules, minimizing travel distances, and reducing operational costs.

Robotics and Autonomous Vehicles: Dijkstra’s algorithm is applied in robotics and autonomous vehicle navigation systems to plan collision-free paths between locations. It helps in ensuring safe and efficient movement of robots and vehicles in dynamic environments.

Supply Chain Optimization: The algorithm is used in supply chain management systems to optimize transportation routes for goods and products. It helps in minimizing shipping costs, reducing delivery times, and improving overall supply chain efficiency.

Emergency Response Planning: Dijkstra’s algorithm is applied in emergency response planning systems to calculate the shortest routes for emergency vehicles, such as ambulances and fire trucks, to reach incident locations. It helps in improving emergency response times and saving lives.

Time Complexity:

The time complexity of Dijkstra’s Algorithm is O((V + E) log V) using a priority queue or min-heap, where V is the number of vertices and E is the number of edges.

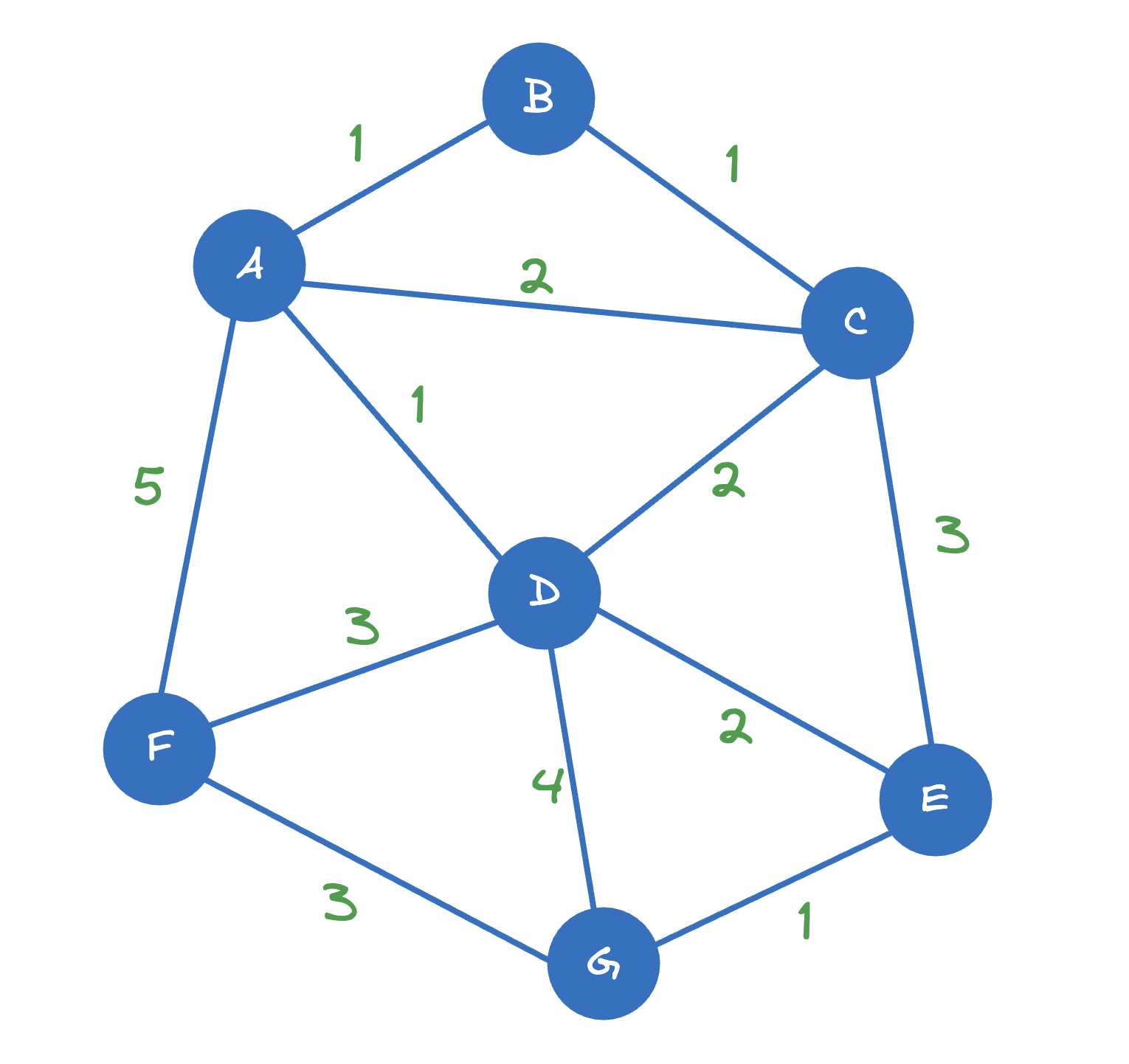
Example:

class Graph {
  private adjacencyList: Map<string, Map<string, number>>;

  constructor() {
    this.adjacencyList = new Map();
  }

  addVertex(vertex: string) {
    if (!this.adjacencyList.has(vertex)) {
      this.adjacencyList.set(vertex, new Map());
    }
  }

  addEdge(vertex1: string, vertex2: string, weight: number) {
    this.adjacencyList.get(vertex1)?.set(vertex2, weight);
    this.adjacencyList.get(vertex2)?.set(vertex1, weight);
  }

  dijkstra(startingVertex: string) {
    const distances: Map<string, number> = new Map();
    const previous: Map<string, string | null> = new Map();
    const priorityQueue = new PriorityQueue();

    for (const vertex of this.adjacencyList.keys()) {
      distances.set(vertex, vertex === startingVertex ? 0 : Infinity);
      previous.set(vertex, null);
      priorityQueue.enqueue(vertex, distances.get(vertex)!);
    }

    while (!priorityQueue.isEmpty()) {
      const currentVertex = priorityQueue.dequeue()!;
      const neighbors = this.adjacencyList.get(currentVertex);

      if (neighbors) {
        for (const neighbor of neighbors.keys()) {
          const distance =
            distances.get(currentVertex)! + neighbors.get(neighbor)!;

          if (distance < distances.get(neighbor)!) {
            distances.set(neighbor, distance);
            previous.set(neighbor, currentVertex);
            priorityQueue.enqueue(neighbor, distance);
          }
        }
      }
    }

    return { distances, previous };
  }

  shortestPath(startingVertex: string, targetVertex: string) {
    const { distances, previous } = this.dijkstra(startingVertex);

    const path: string[] = [];
    let currentVertex = targetVertex;

    while (currentVertex !== null) {
      path.unshift(currentVertex);
      currentVertex = previous.get(currentVertex)!;
    }

    return { path, distance: distances.get(targetVertex) };
  }
}

class PriorityQueue {
  private items: [string, number][] = [];

  enqueue(element: string, priority: number) {
    this.items.push([element, priority]);
    this.sort();
  }

  dequeue() {
    return this.items.shift();
  }

  isEmpty() {
    return this.items.length === 0;
  }

  private sort() {
    this.items.sort((a, b) => a[1] - b[1]);
  }
}

// Example usage:
const graph = new Graph();
graph.addVertex("A");
graph.addVertex("B");
graph.addVertex("C");
graph.addVertex("D");
graph.addEdge("A", "B", 1);
graph.addEdge("A", "C", 4);
graph.addEdge("B", "C", 2);
graph.addEdge("B", "D", 5);
graph.addEdge("C", "D", 1);

const { path, distance } = graph.shortestPath("A", "D");
console.log("Shortest Path:", path); // Output: Shortest Path: [ 'A', 'B', 'C', 'D' ]
console.log("Distance:", distance); // Output: Distance: 4