Depth-first search

Depth-First Search (DFS) is a graph traversal algorithm that systematically explores the vertices of a graph by going as deep as possible along each branch before backtracking. It starts at a chosen vertex, explores as far as possible along one branch, and then backtracks to explore other ones. DFS is commonly used to detect cycles in a graph, topologically sort vertices, and solve problems related to connected components.

How it works:

Step 1: Begin by selecting a starting vertex and mark it as visited.

Step 2: Move to an unvisited neighbor of the current vertex and repeat the process. If all neighbors are visited, backtrack to the previous vertex.

Step 3: DFS can be implemented using recursion or an explicit stack to keep track of the vertices to be visited.

Step 4: Mark each visited vertex to avoid revisiting and use backtracking to explore other branches.

Step 5: Continue the process until all reachable vertices are visited.

Key Characteristics:

Stack-Based (or Recursive): DFS can be implemented using a stack data structure or by recursion. In both cases, it relies on last-in, first-out (LIFO) ordering to keep track of nodes to be visited and backtracked.

Non-Optimal for Shortest Paths: The algorithm does not guarantee finding the shortest path between two nodes in a graph. It explores as far as possible along each branch before backtracking, which may not necessarily lead to the shortest path.

Memory-Efficient: DFS typically requires less memory compared to BFS because it only needs to store the path from the starting node to the current node. This makes it suitable for large graphs or graphs with limited memory.

Completeness (for finite graphs): DFS will visit all the nodes reachable from the starting node in a finite graph. However, it may not terminate in the presence of cycles in an infinite graph without proper cycle detection.

Recursive Nature: DFS is inherently recursive in its nature. When implemented recursively, the function calls itself for each adjacent node until it reaches a leaf node or a node without unvisited neighbors.

Depth-First Search Forest: DFS produces a depth-first search forest, which is a collection of depth-first trees, one for each connected component of the graph. Each tree is rooted at a distinct vertex.

Backtracking Mechanism: DFS employs a backtracking mechanism to explore all possible paths in the graph. When it reaches a dead end (a node with no unvisited neighbors), it backtracks to the most recent node with unexplored neighbors.

Stack Overflow Risk (for recursive implementation): When implemented recursively, DFS may encounter a stack overflow error if the recursion depth exceeds the system’s limit. This risk can be mitigated by using an iterative approach or increasing the stack size.

Applications:

Traversal and Search: Depth first search can be used to traverse and search a graph, visiting all the nodes reachable from a given starting node. This application is useful in scenarios such as finding connected components, identifying cycles, or determining reachability.

Topological Sorting: DFS can be employed to perform topological sorting on directed acyclic graphs (DAGs). Topological sorting is essential in scheduling tasks with dependencies, such as in project management or task scheduling.

Pathfinding: While Depth first sarch does not guarantee finding the shortest path between two nodes, it can be used for pathfinding in scenarios where looking for any path is sufficient. Examples include maze solving, puzzle solving, and navigating game maps.

Cycle Detection: The algorithm is commonly used to detect cycles in a graph. They can be identified when revisiting a node that is already in the current path by maintaining a set of visited nodes and tracking the path taken during traversal.

Strongly Connected Components (SCC): DFS can be applied to find strongly connected components in a directed graph. SCCs are subsets of vertices in a graph where every vertex is reachable from every other vertex within the subset.

Network Analysis: DFS is utilized in network analysis tasks, such as finding bridges and articulation points in a network. Bridges are edges whose removal would disconnect the graph, while articulation points are vertices whose removal would increase the number of connected components.

Solving Puzzles: The algorithm can be used to solve various puzzles, including Sudoku, N-Queens, and word games like Boggle. By exploring all possible configurations or solutions, DFS can efficiently find a valid solution.

XML Parsing and Document Traversal: DFS can be employed in parsing XML documents and traversing hierarchical data structures. It allows for efficient exploration of the document structure and extraction of relevant information.

Decision Trees and Game Trees: DFS is used in decision trees and game trees to explore possible outcomes and make decisions. It helps in determining optimal strategies or paths in decision-making processes.

Backtracking Algorithms: Many backtracking algorithms, such as N-Queens, Subset Sum, and Sudoku solvers, rely on DFS for exploring the search space and finding solutions by systematically trying different combinations.

Time Complexity:

The time complexity of DFS is (O(V + E)), where (V) is the number of vertices and (E) is the number of edges. The algorithm visits each vertex and edge once. Recursive DFS has a space complexity of (O(V)) due to the call stack, while an explicit stack implementation can have a space complexity of (O(E + V)).

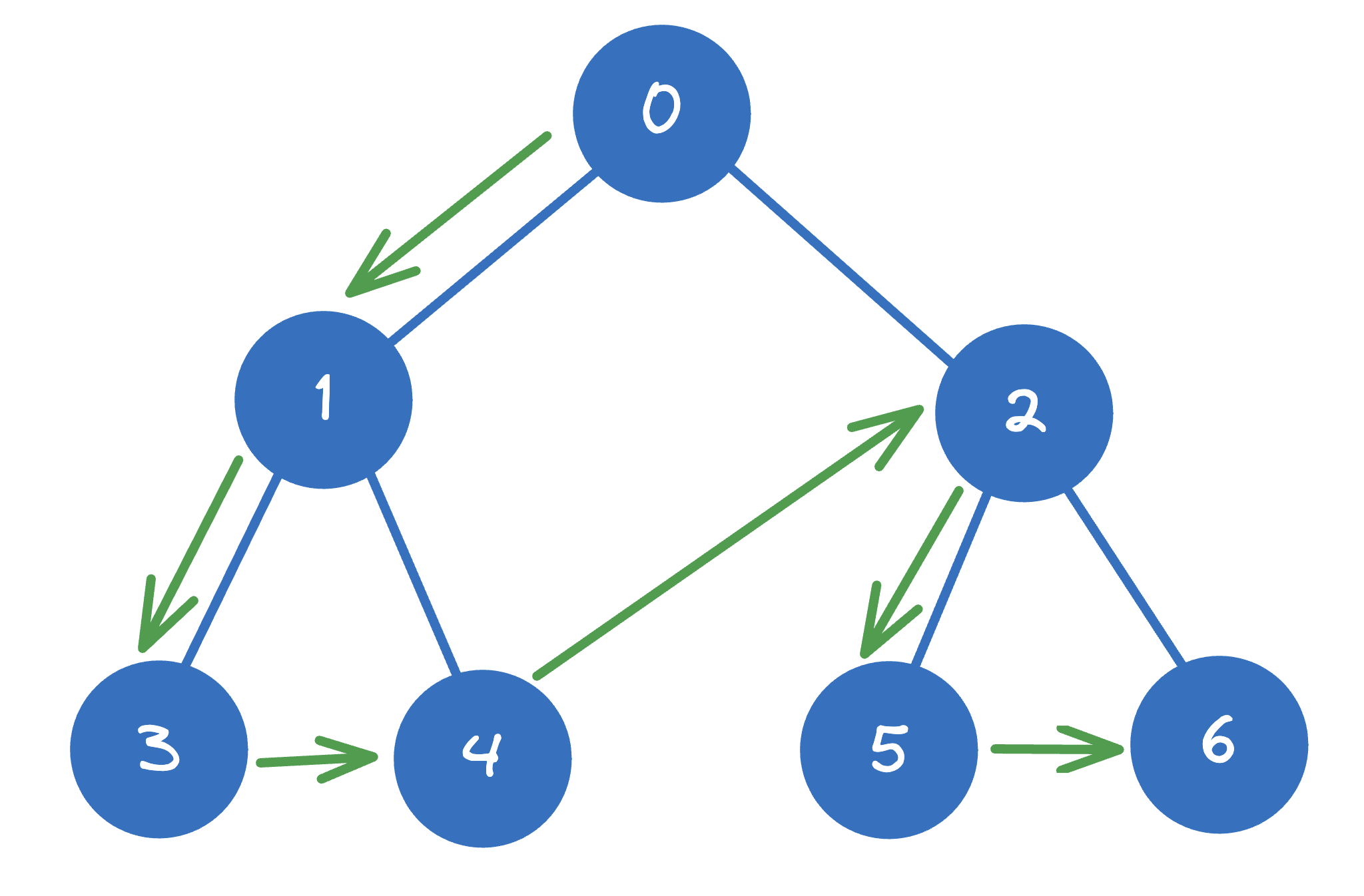
Example:

class Graph {
  private adjacencyList: Map<string, string[]>;

  constructor() {
    this.adjacencyList = new Map();
  }

  addVertex(vertex: string) {
    if (!this.adjacencyList.has(vertex)) {
      this.adjacencyList.set(vertex, []);
    }
  }

  addEdge(vertex1: string, vertex2: string) {
    this.adjacencyList.get(vertex1)?.push(vertex2);
    this.adjacencyList.get(vertex2)?.push(vertex1);
  }

  dfs(startingVertex: string) {
    const visited: Set<string> = new Set();

    const dfsHelper = (vertex: string) => {
      console.log(vertex);
      visited.add(vertex);

      const neighbors = this.adjacencyList.get(vertex) || [];

      for (const neighbor of neighbors) {
        if (!visited.has(neighbor)) {
          dfsHelper(neighbor);
        }
      }
    };

    dfsHelper(startingVertex);
  }
}

// Example usage:
const graph = new Graph();
graph.addVertex("A");
graph.addVertex("B");
graph.addVertex("C");
graph.addVertex("D");
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("B", "D");

graph.dfs("A");